sigmoid function

Sigmoid 函数

Sigmoid函数（也称为Logistic函数）是一种广泛应用于机器学习和深度学习中的激活函数。它是一个平滑的非线性函数，将实数域上的任意输入值映射到0到1之间。Sigmoid函数的数学表达式如下：

σ (x) = \frac{1}{1 + e^{- x}}

其中，x为输入值，e是自然对数的底数（约为2.718）。

图形：

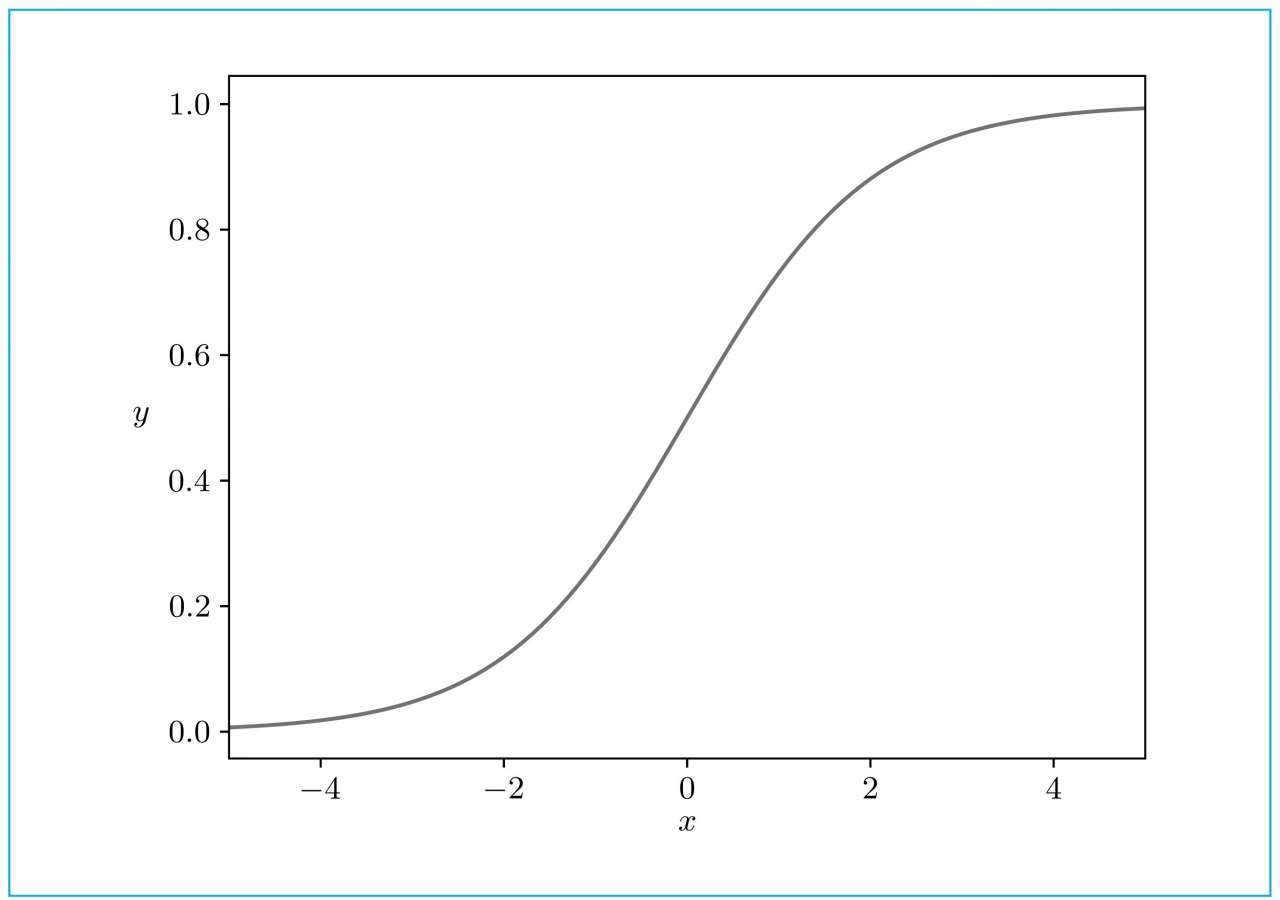
Sigmoid函数具有以下特点：

非线性：Sigmoid函数是一个非线性函数，这使得它在神经网络中的应用可以解决复杂的非线性问题。
易于求导：Sigmoid函数具有较简单的导数形式，这对于在神经网络中使用梯度下降算法进行参数优化非常重要。Sigmoid函数的导数可以表示为：

σ^{'} (x) = \frac{e^{- x}}{(1 + e^{- x})^{2}} = σ (x) (1 - σ (x))

输出范围：Sigmoid函数的输出值在0到1之间。这种特性使得Sigmoid函数在表示概率或用于二分类问题时非常合适。

然而，Sigmoid函数也存在一些缺点，如：

梯度消失问题：当输入值绝对值较大时，Sigmoid函数的梯度接近于0，导致梯度下降过程中权重更新缓慢，可能造成训练过程难以收敛。
非零中心：Sigmoid函数的输出值不是以0为中心的，这可能导致权重更新时的梯度总是具有相同的符号，使得训练过程收敛缓慢。

因为这些缺点，Sigmoid函数在一些深度学习应用中已经被其他激活函数（如ReLU、Leaky ReLU和Tanh等）所替代。然而，Sigmoid函数在某些场景下，如逻辑回归、二分类问题以及输出层需要表示概率时，仍然具有一定的应用价值。

求导

Sigmoid函数的定义为：

S (x) = \frac{1}{1 + e^{- x}}

我们可以通过链式法则来计算其导数。链式法则是微积分中的一个基本法则，用于计算复合函数的导数。首先，我们需要计算S(x)关于x的导数。这可以通过将S(x)分解为两个函数的复合来实现：一个是f(u) = 1 / u，另一个是g(x) = 1 + e^-x。然后我们可以分别计算这两个函数的导数，最后使用链式法则将它们结合起来。

我们来一步步进行：

计算f(u)的导数：f'(u) = -1 / u^2
计算g(x)的导数：g'(x) = -e^-x
应用链式法则：S'(x) = f'(g(x)) * g'(x)

将f'(g(x))和g'(x)的具体形式代入，我们得到：

S^{'} (x) = - \frac{1}{(1 + e^{- x})^{2}} * - e^{- x} = \frac{e^{- x}}{(1 + e^{- x})^{2}}

这就是Sigmoid函数的导数。然而，我们可以进一步简化这个结果。注意到，S(x) = 1 / (1 + e^-x)，所以我们可以将S'(x)重写为：

S^{'} (x) = S (x) * \frac{e^{- x}}{1 + e^{- x}} = S (x) * (1 - S (x))

这就是Sigmoid函数导数的最终形式，它表明了Sigmoid函数的一个重要性质：它的导数可以用函数自身来表示。这在计算梯度时非常有用，因为我们已经计算了S(x)，所以可以直接用它来计算导数，而无需再次计算e^-x。

本文作者：Maeiee

本文链接：sigmoid function

版权声明：如无特别声明，本文即为原创文章，版权归 Maeiee 所有，未经允许不得转载！

喜欢我文章的朋友请随缘打赏，鼓励我创作更多更好的作品！